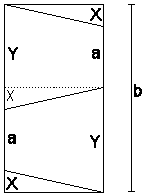Zunächst versetzt man die beiden Trapeze gegeneinander, wie auf der Skizze zu sehen. Jede der langen Seiten (b) des Stoffes besteht nun aus dem halben Hüftumfang (a), der Kante des Verschnittstückes (X) und dem halben Saum (Y). Bei (a) sollte man bedenken, dass dazu ein paar zentimeter Nahtzugabe zu rechnen sind und dass man beim Anziehen an der Hüfte vorbei muss.
Es gilt also: b=a+X+Y
Da die beiden Trapeze ja in sich symmetrisch sind, die Seiten also die gleichen Winkel und Längen haben, gibt es auf der einen Seite von a ein reales X, auf der anderen sozusagen ein 'virtuelles'. Zur Verdeutlichung siehe die Punktlinie, die keine Schnittlinie sein wird.
Wir erkennen: Y=a+2X
Somit haben wir für unsere beiden Unbekannten X und Y zwei Gleichungen. Da die eine bereits nach Y aufgelöst ist, tun wir dasselbe mit der anderen (links allgemein, rechts mit den Beispielzahlen a=50 cm (halber Hüftumfang) und b=205 cm (Stofflänge):

b=a+X+Y	205=50+X+Y
b-a-X=Y	155-X=Y
Wir setzen mit Y=a+2X gleich und lösen nach X auf:
b-a-X=a+2X	155-X=50+2X
b-a=a+3X	155=50+3X
b-2a=3X	105=3X
X=(b-2a)/3	X=105/3=35

Das nun bekannte X kann dann wie a in Y=a+2X eingesetzt werden, im Beispiel Y=50+70=120. Der Saum wird also im Beispiel nach Vernähung knapp 240 cm Umfang haben. Das stellt auch den Herrn (oder die Dame) mit langen Beinen und großen Schritten zufrieden.
Wenn ihr nun einen anderen halben Tallienumfang oder eine andere Stofflänge habt, braucht ihr nur die Werte entsprechend für a und b einzusetzen und das alles nochmal neu nachzurechnen.

Nachdem die beiden Hälften aneinandergenäht waren, habe ich Y jeweils zur Naht hin noch etwas abgerundet, damit die Seiten nicht länger sind als vorn und hinten.

Was bin ich für eine Labertasche! Ich hoffe, es ist niemand eingeschlafen oder an Mathematikangst verstorben.